|
|
|
|
|
A note from 2007 on an incorrect inductance formula
Wheeler's long-coil formula is adequate for many engineering
calculations when  /D ≥ 0.4;
and his continuous formula is both highly accurate and manageable
using a scientific calculator. That does not stop people from
looking for alternatives to it however, sometimes with unfortunate
consequences. One such alternative was given hy Hank Meyer [see
reference below]; on the basis that Wheeler's long-coil formula
did not agree with his measurements (the real problem being that
he used the diameter of the coil former instead of the mean diameter
of the coil): |
|
D ≥ 2 |
kL = 0.9694(D/)-0.6932 |
 |
|
2 ≥ D |
kL = 0.9617exp{-0.2913(D/)} |
|
|
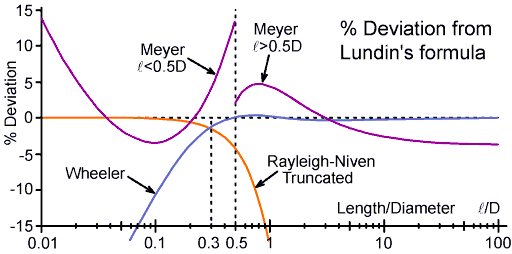
where exp{x}=ex Using Lundin's handbook formula as datum, a comparison between this formula and Wheeler's long-coil formula is shown in the graph below: |
|
Meyer's long-coil formula (for >0.5D)
is grossly inferior to Wheeler's long-coil formula (which it
claims to supplant) and has no merit whatsoever. The short coil
formula (for <0.5D)
however offers an accuracy of ±5% in the /D
range from 0.02 to 0.3, and so might appear to have some utility
as a crude approximation were it not for the fact that a far
better simple formula already exists. The curve marked 'Rayleigh-Niven
truncated' is obtained by using only the first two terms of the
Rayleigh-Niven formula. This was reproduced in Meyer's article
as part of an erroneously transcribed version of Coffin's formula,
i.e.: kL = (2/π)( /D)[
ln(4D/) -½ ]and so he should have been aware of it. If this formula is used for /D up to 0.3, and
Wheeler's long-coil formula us used for /D
greater than 0.3, the maximum error is about 1.5%. This is still
poor of course, and Wheeler's 1982 unrestricted formula (which
was known at the time) is generally to be preferred.What is particularly problematic about Meyer's approximation is that it has been used in at least one computer program distributed to Radio Amateurs. Its accuracy in the most important region from /D=0.3
to 3 is lamentable; and its promotion as an alleged improvement
over Wheeler's formula makes it necessary to inspect the source
code or otherwise verify the accuracy of inductance calculation
programs obtained via the Amateur Radio community. It cannot
be stressed too strongly, that when coding a program, there is
no excuse for using crude approximate formulae. |
|
Reference: "Accurate Single-Layer-Solenoid Inductance Calculations", Hank Meyer W6GGV, QST Technical Correspondence, April 1992, p76-77. "Corrections to Accurate Single-Layer Solenoid Inductance Calculations", Hank Meyer. QST July 1992, p73. Complains of inaccuracy of Wheeler's formula, but fails to appreciate that Wheeler's formula is a current-sheet approximation. Confuses coil-former diameter with coil diameter. Fits Nagaoka's coefficient (taken from Langford-Smith's graph) to simple functions, but these functions are seriously inaccurate in the region of interest. The long-coil formula is far less accurate than Wheeler's formula, and the short-coil formula is less accurate than truncating the Rayleigh-Niven formula to a single term. Equation 4, for Rosa's mutual inductance correction is only accurate to 20.6% and does not return 0 when N=1. Computer programs developed from this article should be avoided.  Additional
errata: April: Eq.5 is not Nagaoka's coefficient, it
is formula (119) from [Grover 1946] p143. This formula is a truncated
version of Coffin's formula with a transcription error in the
second term. The second term should read ...+ (B²/8)[ln(4/B)
+ 1/4]-... (see erratum of [Grover
1946]. Meyer adds his own transcription error also: the last term of Eq. 5 should be (5B6/1024){...}. Eq. 6 is not Nagaoka's coefficient, it is the Webster-Havelock formula [Grover 1946] p 121). The accuracy of Eq. 5 without corrections is 0.66% and Eq.6 is 0.06%, not one part in 105 as stated. April: Ref 3 should read pp1-33. July p73: The statement that inductance is independent of frequency is incorrect. |
© D W Knight 2007, 2010, 2016.
|
|
|
|
|
|